Book review: Bastiat: The Law

 The Law by Bastiat is recommended by various Libertarian leaning folk such as EconLib. So I decided to read it. However, I was somewhat disappointed. Perhaps quoting from the start will help explain:

The law perverted! And the police powers of the state perverted along with it! The law, I say, not only turned from its proper purpose but made to follow an entirely contrary purpose! The law become the weapon of every kind of greed! Instead of checking crime, the law itself guilty of the evils it is supposed to punish! If this is true, it is a serious fact, and moral duty requires me to call the attention of my fellow-citizens to it.

It is all rather polemical. His complaint is revealed in the section The Complete Perversion of the Law: that unfortunately, law by no means confines itself to its proper functions. I agree with pretty well all he says but don't find it to be helpfully well said; Hayek I think says such things better. But if you've never read H or his ilk, this might be interesting.

Newton on diffraction

I'm reading - well, browsing; or perhaps skipping - Principia Vol 1, and am in the middle of a rather tedious part where he proves various uninteresting results about attractions of spheres and so on in great detail. Section XIV (The motion of very small bodies when agitated by centripetal forces tending to the several parts of any very great body) Proposition XCIV Theorem XLVIII is:

If two similar mediums be separated from each other by a space terminated on both sides by parallel planes, and a body in its passage through that space be attracted or impelled perpendicularly towards either of those mediums, and not agitated or hindered by any other force; and the attraction every where the same at equal distances from either plane, taken towards the same side of the plane: I say, that the sine of incidence upon either plane will be to the sine of emergence from the other plane in a given ratio.

And the proof is (note: you may not want to read the proof, whose details do not concern us, or the scholium that follows; try reading my final para first):

CASE I. Let Aa and Bb be two parallel planes, and let the body light upon the first plane Aa in the direction of the line GH, and in its whole passage through the intermediate space let it be attracted or impelled towards the medium of incidence, and by that action let it be made to describe a curved line HI, and let it emerge in the direction of the line IK. Let there be erected IM perpendicular to Bb the plane of emergence, and meeting the line of incidence GH pro longed in M, and the plane of incidence Aa in R; and let the line of emergence KI be 6 produced and meet HM in L. About the centre L, with the radius LI, let a circle be described cutting both HM in P and Q, and MI produced in N; and, first, if the attraction or impulse be supposed uniform, the curve HI (by what Galileo hath demonstrated) will be a parabola, whose property is that of a rectangle under its given latus rectum, and the line IM equal to iare of HM; and moreover the line HM will be bisected in L. Hence ro MI there be let fall the perpendicular LO, then MOW, OR will be equal; and adding the equal lines ON, Ol, the wholes MN, IR will be equal also. Therefore since IR is given, MN is also given, and the rectangle MI MN is to the rectangle under the latus rectum and IM, that is, to HM in a given ratio. But the rectangle MI MN is equal to the rectangle MP MQ, that is, to the difference of the squares ML², and PL² or LI²; and HM² hath a given ratio to its fourth part ML²; therefore the ratio of ML²-LI² to ML² is given, and by conversion the ratio of LI² to ML², and its square root, the ratio of LI to ML. But in every triangle, as LMI, the sines of the angles arc proportional to the opposite sides. Therefore the ratio of the sine of the angle of incidence LMR to the sine of the angle of emergence LIR is given. Q.E.D. [Note: in this pic, the planes Ae and Bb are really parallel despite what my rubbish photo might appear to show.]

CASE 2. Let now the body pass successively through several spaces terminated with parallel planes AabB, BbcC, &c., and let it be acted on by a force which is uniform in each of them separately, but different in the different spaces; and by what was just demonstrated, the sine of the angle of incidence on the first plane Aa is to the sine of emergence from the second plane Bb in a given ratio; and this sine of incidence upon the second plane Bb will be to the sine of emergence from the third plane Ce in a given ratio; and this sine to the sine of emergence from the fourth plane Dd in a given ratio; and so on in infinitum, and, by multiplication of equals, the sine of incidence on the first plane is to the sine of emergence from the last plank in a given ratio. Let now the intervals of the planes be diminished, and their number be infinitely increased, so that the action of attraction or impulse, exerted according to any assigned law, may become continual, and the ratio of the sine of incidence on the first plane to the Sine of emergence from the last plane being all along given, will be given then also. Q.E.D.

Aaaanyway, the point is that this is all very dull: who cares other than as an abstract curiosity about motion in such a gap? And it isn't the end of it; he goes on to prove some more. The answer is given by the Scholium at the end:

These attractions bear a great resemblance to the reflections and refractions of light made in a given ratio of the secants, as was discovered by Snell; and consequently in a given ratio of the sines, as was exhibited by Descartes. For it is now certain from the phenomena of Jupiter's satellites, confirmed by the observations of different astronomers, that light is propagated in succession, and requires about seven or eight minutes to travel from the sun to the carth. Moreover, the rays of light that are in our air (as lately was discovered by Grimaldi, by the admission of light in a dark room through a small hole, which I have also tried) in their passage near the angles of bodies, whether transparent or opaque (such as the circular and rectangular edges of gold, silver, and brass coins, or of knives, or broken pieces of stone or glass), are bent or inflected round those bodies as if they were attracted to them; and those rays which in their passage come nearest to the bodies are the most inflected, as if they were most attracted; which thing I myself have also carefully observed. 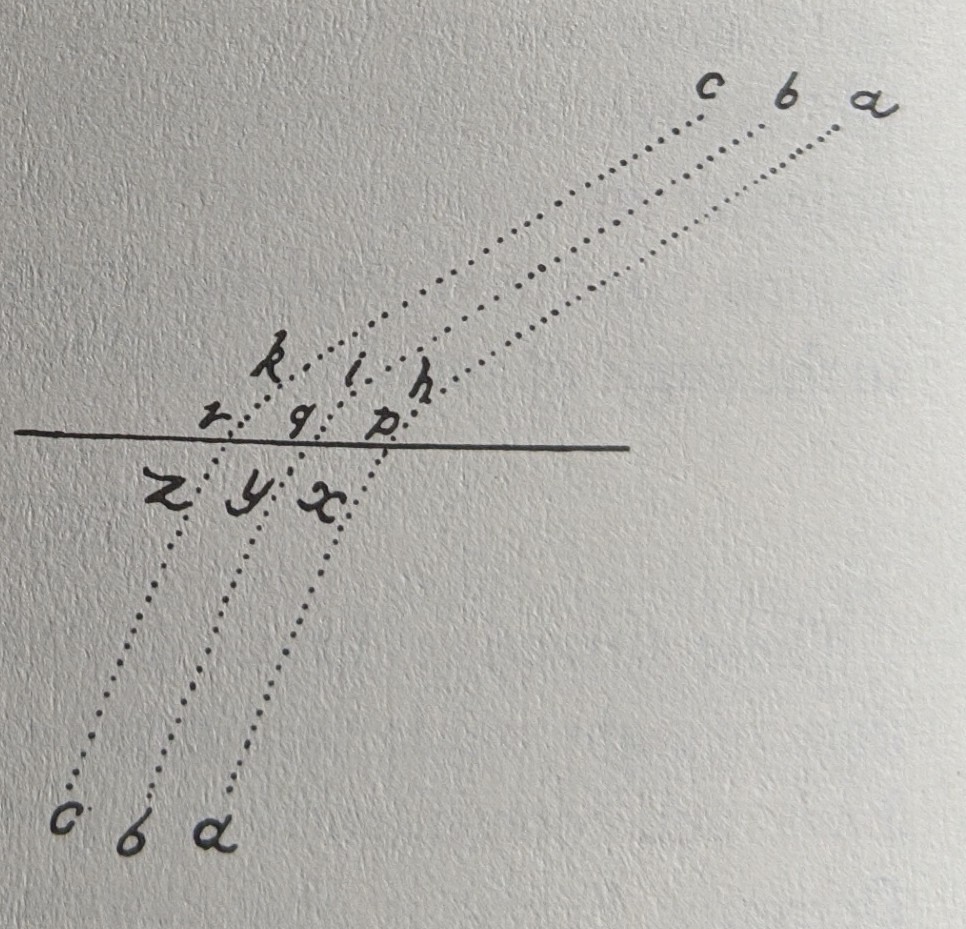And those which pass at greater distances are less infected; and those at still greater distances are a little inflected the contrary way, and form three fringes of colors. In the figure s represents the edge of a knife, or any kind of wedge AsB; and gowog, fnaf, meme, dsld are rays inflected towards the knife in the arcs owo, non, mom, Ist; which inflection is greater or less according to their distance from the knife. Now since this inflection of the rays is per formed in the air without the knife, it follows that the rays which fall upon the knife are first inflected in the air before they touch the knife. And the case is the same of the rays falling upon glass. The refraction, therefore, is made not in the point of incidence, but grad ually, by a continual inflection of the rays; which is done partly in the air before they touch the glass, partly (if I mistake not) within the glass, after they have entered it; as is represented in the rays cxc, bipi, ahxa, falling upon r, q, p, and inflected between k and z, i and y, h and x. Therefore because of the an alogy there is between the propagation of the rays of light and the motion of bodies, I thought it not amiss to add the following Propositions for optical uses; not at all considering the nature of the rays of light, or inquiring whether they are bodies or not; but only determining the curves of bodies which are extremely like the curves of the rays.

Enough of this Newton clown, what about me?

So, he is trying to understand what will come to be called diffraction (not in the coplanar bit; which is analogous to refraction; I mean in in the bulk of the Scholium). FWIW, this casts some doubt on whether he has indeed observed this stuff himself, or is only relying on others. But more importantly, he's wrong, because diffraction is the wave-like nature of light coming out, and Newton believes in a corpuscular theory. This is minorish; these were early days for a theory of light, people were getting things wrong, and the "true" aka QM view is waaay out of his reach. But nonetheless I think he can know his theory is wrong, by about the one thing he doesn't try to do, which is to try to quantify it - which is common to much of the volume. He knows - or he could know, if he cared to look - that light is not bent to any measureable degree by the gravitational fields of anything as tiny as a piece of glass. But if he admits that, he has no theory at all for diffraction, which would annoy him.

And on the tides

Apparently from nowhere, he pulls out the third power law. This is suspicious (or did I miss something). Did he understand the reason or just somehow guess it? If he understood, I would have expected him to expound on the reasons in some detail. As the book's notes point out, he then tries to deduce the relative density of the moon, but gets it wrong by a factor of two, because he uses the ratio S - L / S + L, but doesn't realise that it is All Very Complicated, especially in channels. But he could have suspected that, and used values from mid-Atlantic islands, perhaps?

And on novae

At the end of the section on comets, he notes that some come very near the sun, and will inevitably eventually fall in. He then speculates that at the other end of their orbits - I think; but he could have meant around other stars; but I think he doesn't realise there's an Ooort cloud, he takes them more generally spread - some fall in, and nourish failing stars, and cause novae. Which is of course wrong, comets are far too small and so on, but it is an interesting idea.

Ecrins 2020: Saturday and Sunday: Home

Pack up and off, though I forget exactly when. It's about 5:30 from Vallouise to Dijon - we'd done our usual break-somewhere-now-where-shall-we-choose and picked Dijon, the name at least is good - and we got there around 5, with stops at the Col du Lautaret and <somewhere else>, so I'll guess we left around 10.

Dijon was... disappointing, I'm sorry to say. We arrived, found somewhere to park, checked in, and found we'd just missed the Cathedral closing time, which was regrettable; and then somehow there wasn't much else to see. It didn't help that it was bakingly hot. Sitting in the shade in a courtyard on the other side of, and contemplating, the cathedral helped a bit. My recollection is thta it wsan't easy to find anywhere decent for dinner, either.

Our appt for the night at "City Loft" was good though: lots of space, central, and in a nice "turret" like the one opposite.

But our lunch stop in Saint Quentin made up for Dijon.

Spot the Panda.

One last steak tartare. D looks elegant in my hat.

Drive, tunnel, all fine. And then, all of a sudden, we were home.

Ecrins 2020: Thursday and Friday: Col d'Arsine

We have, alas, pretty well come to the end of our time. We have one more "night up" available, and decide to camp out, since it was fun last time and the Wx looks good. This discards the "Pelvoux" plan, but that was but a sketch, and anyway we feel like something lighter: we're... well, we feel like we've worked, let us say. We might go to the Lac de la Muzelle, but that's a longish drive, so instead opt for the Col d'Arsine, which dovetails nicely with what we've done already: we've looked down on it often enough.

GPS trace: Le Casset up to camp at col d'Arsine.

But before that, there's time to admire the sun rising over The Hill again; this time I notice there's a line of three "holes" just L of the sun.

Before it gets too hot E and I go for a little walk, down to the valley then out, past the Chalet des Trolls

which is still beautifully situated, but if anything I now prefer our current place. But C-des-T would accommodate more people. Walk along the river a ways, to a bridge, then back. Find a house with beehives in it's attic. Talk of houses and things we remember from last time. To the weekly market.

pm: drive round via Briancon to Monetier then Le Casset, park - in shade! - and walk into the village; find a cafe by a bridge and the church, and an odd totem-pole which I think I remember.

If that looks oddly deserted, recall that it is hot, and anyone wiht any sense is hiding in the cool shade of the cafe. After a few rounds and drink, we go a bit further into the village, over the next bridge which is the right bridge, and up into the forests. since it is now lateish pm, we "bonjour" a stream of people coming down. I recall my trip through here a few years back, and so don't take many pix this time. Here's D+E walking up, and resting at the Lac de la Douche. And so up the steep but good scree path, and then the long pleasant uphill by the side of the stream, past the berger's cabane, and a little bit higher to nearly the col, while it is still light.

Find a nice spot, on our own; there are a few others lower down. Settle down: elect to put up tent, even though Wx fine, since there's a breeze. Make porridge, despite me forgetting the spoons - and quite a bit else - the cap from the gas cylinder works as a spoon; stir in some trail mix.

A few more rounds of cards; reading; the light fades; good night. Smilier D.

Friday

Sleep well. tent is fine for the three of us. Up ~7 just as the sun is getting onto us - should we have camped actually at the col, to get the light earlier? B'fast porridge &c, pack up tent fairly promptly and head up to the two lakes, a little higher, via an obscure path. And so to the lakes. There's a curious man-made channel connecting them, which we ponder briefly. Stare up at the surrounding cirque and work out where we've been. Then head down back to path and packs. Pic: possibly pic de Neige Cordier; certainly, the moon. Context.

GPS trace.

D and E will go on, to Villar d'Arene; I go back to the car and go round to pick them up. Stroll back in no great hurry; enjoy peace and solitude. Pic: to Agneaux.

The merry stream, and a trail of sheep.

Just below le lac, looking up N to le glacier du Casset, on the Agneaux.

Drive to Villar d'Arene is further than I thought, but I get there a little before D+E. It's a pleasant place, perhaps somewhat faded, I make the mistake of driving into it but get away with it, just.

Sit down in a cafe in the main square and await D+E, who arrive; and we return. D is exhausted.

Late pm: I drive up to Ailefroide just to find some climbs; see GPS trace. I do find them; see pix starting around here. Next time, we must do valley climbing more seriously.

Ecrins 2020: Tuesday and Wednesday: mostly rest

[Notes : Arrival : Ref des Bans : Lac d'Eychauda / Pic du Rif : Rest : Ref Gl Blanc; Montagne des Agneaux : Pic du Gl d'Arsine to Ref des Ecrins : Pt Louise]

Tuesday: Up a little later than normal. Sit outside with muesli and a succession of coffees. It's a bit windy: I have to stop the parasol from blowing away. We're all in need of rest, so do nothing all day except I go down to town for bread; and mid-pm I make my long-promised trip up to Puy St Vincent to see if it would be a suitable place to stay in future years. In short, no. In long: there is stuff up there, but quite thin; we'd have found ourselves coming down to Vallouise a lot, and it is too far to walk quotidien. The church you see from Vallouise is no longer a church (also). Local map. View up to PSV from our terrace.

But you do get a decent view down to Vallouise and across. There's a "table d'orientation" type thing, from which I think I deduce that the skyline on the L is les Agneaux.

Soir: eat in: bread, cheese, pate, fougasse-a-chevre. Here's Vallouise-in-general, and below is zoomed to Our House.

The four 2-storey appts in the center; we're the lower-left-front one.

Wednesday: another mostly rest day, though we did attempt to climb in the afternoon. Up 7:30, sneak through l'room to avoid waking D, take muesli and juice outside. the sky is pure blue, the air is chill - the sun not yet over The Hill - I have my fleece on. Lovely. Browse the wub - SpaceX SN5 first hop - and end up on Citizens United. Popper, ch 6 and start ch 7, on how the fundamental Q is not "who should rule" but rather how to limit power. Coffee; some of y'day's baguette de tradition. D up; then E; she comes out to read P and we discuss her disagreement with my view that P's assertion of a racial aspect to Pl's classes is right. 11: E to town for bread; I wash up.

pm: to Pas du Loup for a nice easy 6 pitch 4c route at Bouchier. There's a cafe / gite / refuge and we play a few hands while waiting for the sun to go round. It was slow and dusty and slightly iffy driving up once off the main road. We watch a party on some-other-route. We're not quite sure where ours is; doubtless it will become clear as we get closer.

But, it doesn't. After heading up the right path all becomes doubtful, and we end up scrambling around on scree and boulders, and too close to see where we are, and nothing matches and there are no bolts. We could perhaps have been bold and just climbed <anything> since it seems quite climbable, but the children resisted my blandishments and perhaps that would better be done earlier in the day. Eventually, give up and go down and take the path round to the top, which is a pleasant path. We poke around, find some bolts and some markers ("R" for relais, perhaps?).

When driving out, stop and look, and finally have enough perspective: those other people were on our climb; ah well. Compare to the closer view.

Dinner: Argentiere-la-Besse, with cats.

Ecrins 2020: Monday: Pt Louise and down

[Notes : Arrival : Ref des Bans : Lac d'Eychauda / Pic du Rif : Rest : Ref Gl Blanc; Montagne des Agneaux : Pic du Gl d'Arsine to Ref des Ecrins] Today's GPS trace

Today's intent is the S arete of Pt Louise, which M and I did so many years ago. E and I up at 7, D somewhat later. Last night M. le Guardian had performed le Meteo and it was not encouraging; cloud, and high wind. The morning Wx is not obliging, though quite still, and the infants are dubious, so we settle for the snow way.

The way up is cloudy but easy. Mostly snow, a rock band at 2/3 height, and a rock ridge to the summit. Views off the far - N - side are dramatic and weird.

Occasionally we can almost see the Barre.

Summit selfie.

Snow conditions were fine, descent too. Pano, near/at top.

View back up, on the way down.

And so down, and pic up sacs, and head off. We do descend via the "glacier route" and it is easier, and there are nice crevasses. Notice that we're being good and wearing the rope; partly because we already had it on for Pt Loiuse.

And so down the Ref Gl Blanc.

And down... pano overlooking le Pre du Madame Carle; Glacier Noir to R.

Find car, E removes banana skins, and we tootle off. Dinner in les Vallois.

Ecrins 2020: Sunday: Pic du Gl d'Arsine to Ref des Ecrins

[Notes : Arrival : Ref des Bans : Lac d'Eychauda / Pic du Rif : Rest : Ref Gl Blanc; Montagne des Agneaux] Today's GPS trace

Up in no great hurry and trundle off. Here's the quiet dortoir after everyone else has left. The Pelvoux is still glorious; we'll get there one day, Miranda must have her dream!

In the light of day the route of yesterday is clear to start: just along (actually a bit behind and below) that moraine line, into the snow, and up around the corner.

The route up to the Ecrins is definitely over glacier even if you take the "easy" way, and so gets a go-back-home-children warning sign. We do take the easy route, because why not; and anyway, we're going to the Col du Gl Blanc. Although all it is, is a path over moraine / rubble / rock as an alternative to the glacier's crevasse zone; though that doesn't look so bad this year. We'll probably do the glacier in descent.

We're high enough to see into the main Gl Blanc basin, Barre at the end, and if you know where to look the Ref des Ecrins on the R. The view back down from that point is gorgeous too. In fact it is all gorgeous: why don't I live there?

Once we're tolerably sure we're below the right point for the Col, we go a little off the path, leave our sacs in a place hopefully obvious from above, and head up. It is F, so no axes or crampons. Looking at the GPS trace will probably make it clear. we make it to the Col easily enough, with views over the far side to the lacs d'Arsine. Which looks a bit of a wasteland, but the valley just beyond is pleasant and green, and has the GR54 in it; we'll camp there in a week or so.

from the Col to the Pic du Gl d'Arsine is an easy scramble that we all enjoy. And have a nice rest on the summit (3364) though it's going a bit grey.

Behind: L of E, Agneaux. somewhat R of D, Pic du Rif and stuff. Summit selfie. And looking back to the Col (3275) with the Neige Cordier behind it.

Getting down is fairly easy, but E in particular wished we'd brought crampons, or axes, or preferably both. We even manage to find the rucksacs, that we thought we'd left so clearly visible. See if you can see D's big dark blue one.

And so on up the the familiar Ref des Ecrins, and I'll spare you the last 20 mins of grind up the path off the glacier, always such fun to look forward to. Though D and I took a recce up the glacier a little ways to look at Pointe Louise and the descent for tomorrow (due to seracfall or whatevs, the Barre is currently deconseilee, so we've settled on Pointe Louise for tomorrow, which will ease D's unlove of early mornings).

View of the inside of the Ecrins.

The Guardian offers us 4 am for Pt Louise but I cunningly counter-propose 6, and we settle on 7:30, which should give us time, if the Wx looks OK, which is currently iffy. Sort through kit: have I stripped the gear down too much?